こんにちは、いのっちです。
今日は人間がものを見るとき、塊としてまとめて知覚してるよという話。
そう、ゲシュタルトの法則をご紹介します。
ゲシュタルトの法則とは
人がものを見て知覚するとき、無意識の内にまとめてみる特性があり
それが起こる際の法則をゲシュタルトの法則といいます。
ゲシュタルトの法則は下記の7つがあります。
ゲシュタルトの法則
1.近接 (Ploximity)
2.類同(Similarity)
3.連続(Continuity)
4.閉合(Closure)
5.共通運命(Common Fate)
6.面積(Area)
7.対称性(Symmetry)
さて、どんなものか見ていきましょう。
近接 (Ploximity)
距離が近いものをグループとして認識します。
↓の画像を御覧ください。どのように見えますか?

きっと、このようなグループであると感じたのではないかと思います。
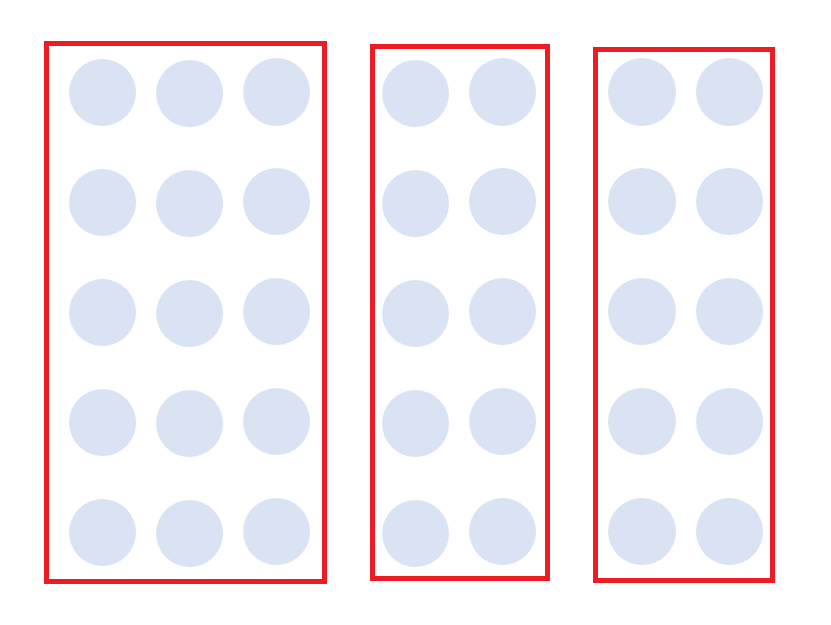
類同(Similarity)
類同は色、形、向きなどが同じものをグループとして認識します。

上の画像も↓のように感じますよね

連続(Continuity)
連続は線を見た時、変化や切れ目がない1本の線としてみることです。
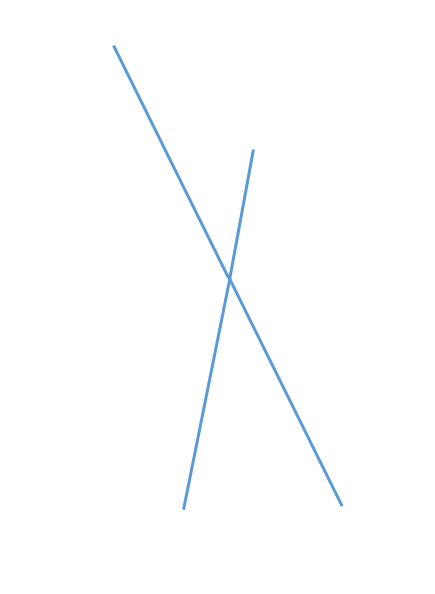
この画像はどう見えますか?
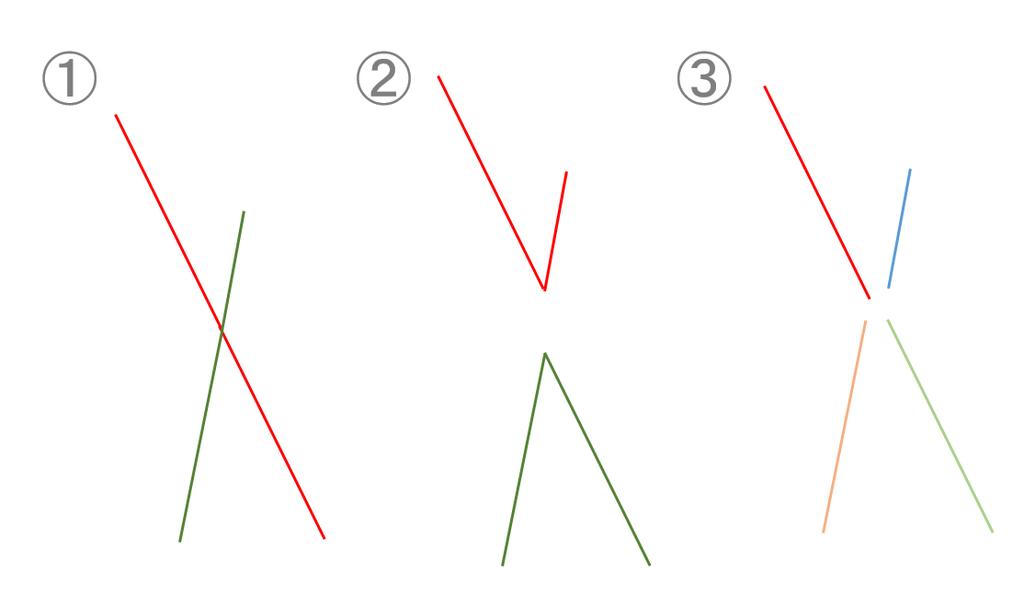
きっと、①のような2本の線に見えたのではないでしょうか。
②や③のような線が集まっているようには感じられなかったと思います。
閉合(Closure)
閉合は閉じた形をみたときに1つのグループとしてみることです。
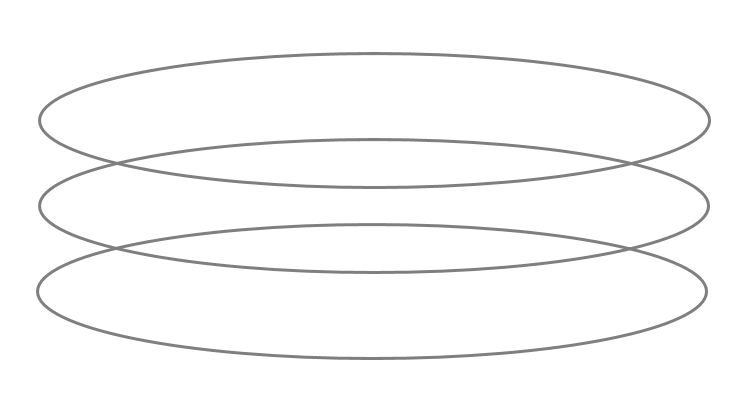
それでは見てみましょう!
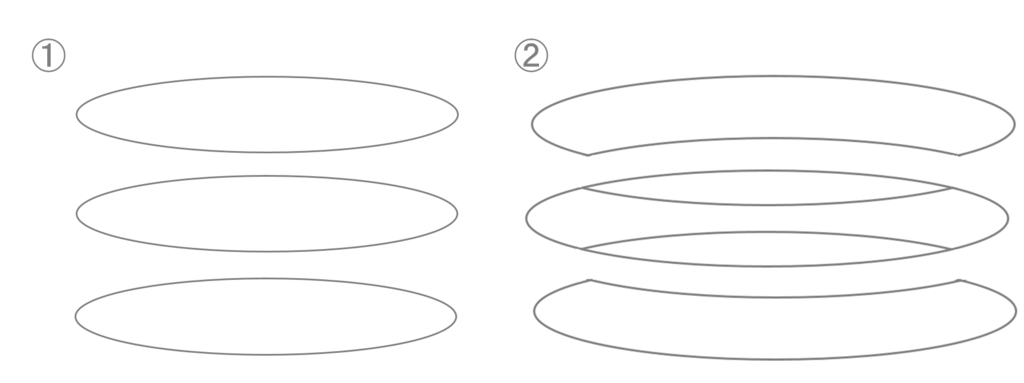
これも①のような3つの楕円が重なっていたように見えますよね。
②のような欠けた楕円と模様の入った楕円であるとは思わなかったのでは無いでしょうか。
共通運命(Common Fate)
移動の方向や点滅などの周期が同じであるものをグループとしてみることです。
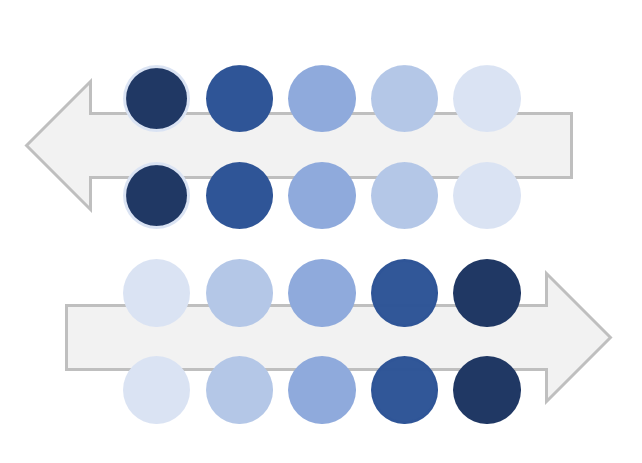
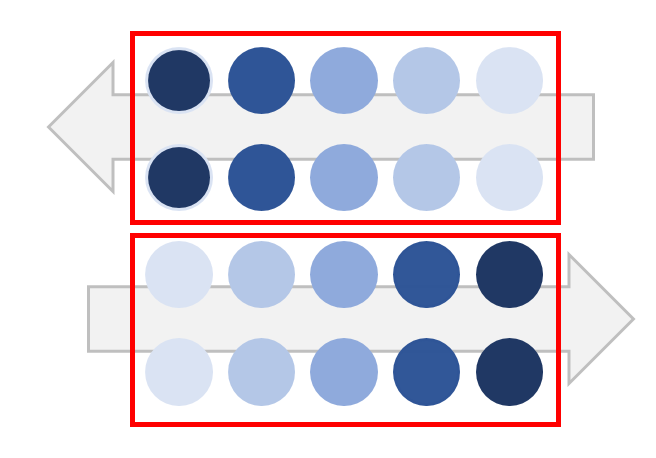
上2つのマルが左、下2つのマルが右に動いている場合、↓のようにグループ化して見てしまいます。
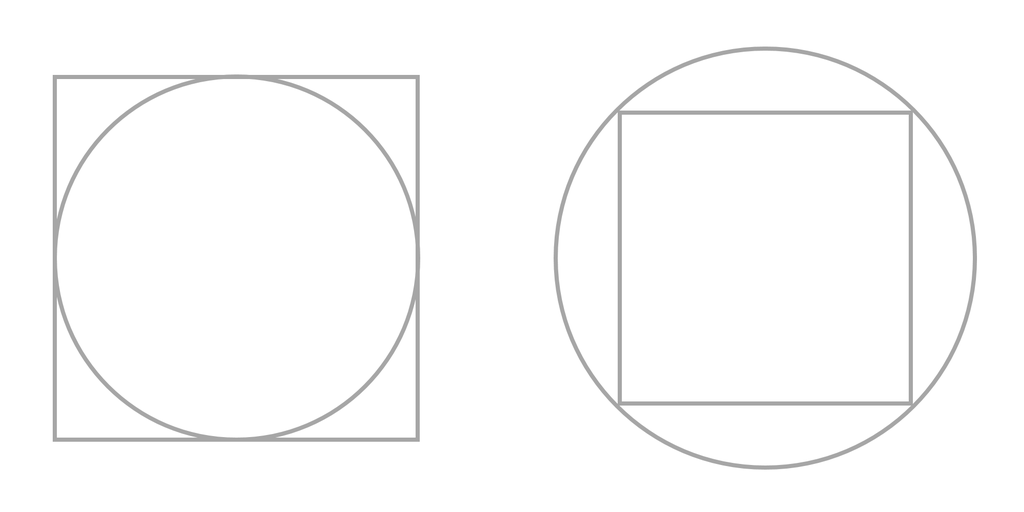
面積(Area)
図形の中に図形がある場合、中の図形をメインの図形として認識します。
対称性(Symmetry)
左右対称のものには、何らかの意味を見出してしまいがち
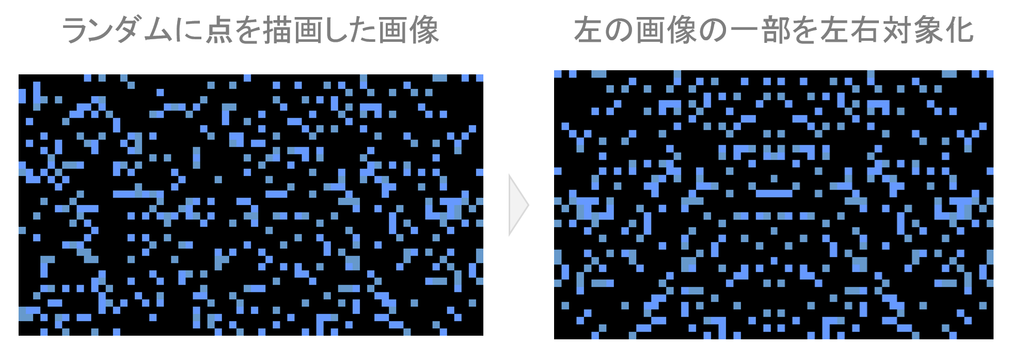
生成したランダムドットの画像(左)を加工して、左右対称化した画像(右)を作りました。どこか気になる点はあるでしょうか。
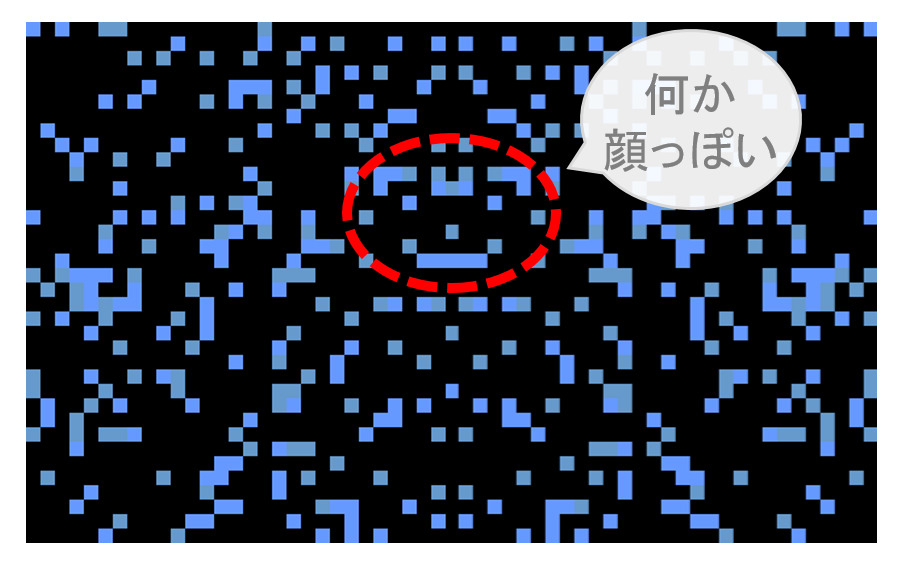
円で囲んだ部分、何か顔に見えてきません?
顔があると、なんだか意味のある画像に思えてきます。
最後に
実は「ゲシュタルト」って言いたかっただけなんです。
なんか、中二っぽくてかっこいいですよね。
ゲシュタルト。
ゲシュタルトの法則は日常のデザインの中でよく使われています。
皆さんの身の回りのものを法則に照らし合わせ、「あっ、あれは○○の法則だな」とニンマリしてみると、楽しくデザインについて素養がつくと思います。ぜひお試しを。
\\ 『明日のはたらくを創る』仲間を募集中!! // 919.jp